 |
Пропустим вступление об аддитивных и мультипликативных моделях, т.к. оно представляет теоретическую базу, с которой можно ознакомиться в самой статье и начнем с анализа алгоритма прогнозирования объемов продаж. В результате анализа алгоритма, в первой части статьи будет предложен его доработанный вариант.
Вторым разделом статьи будет использование доработанного алгоритма на примере, который предоставил Кошечкин С.А.
1. Определение тренда. Первым шагом в построении модели является выбор линии тренда. Автор утверждает, что выбор полиномиальной линии тренда дает наиболее точную модель, опираясь на коэффициент детерминации, как критерий оценки всей модели в целом. Однако он пропускает тот факт, что точность модели зависит не только от ошибок моделирования тренда, но и от ошибок моделирования сезонных колебаний. Другими словами, модель F=T+S+E (F — значения модели, T — значения линии тренда, S — значения сезонной компоненты, E — величина ошибок) зависит от двух ключевых параметров Т и S, а не только от Т, как утверждает автор. Параметр Е определяет доверительный интервал модели и дает возможность анализировать точность построенной модели.
Выбор наиболее точной линии тренда (Т) с высоким коэффициентом детерминации не является достаточным условием построения оптимальной модели. При росте коэффициента детерминации уменьшается ошибка тренда, но не модели в целом. Таким образом, автор отсекает альтернативные модели, утверждая, что они заранее менее точны, опираясь при этом на данные анализа одного параметра всей модели — тренда (T).
2. Определение величин сезонной компоненты. Необходимо учитывать также ошибки сезонных колебаний (S), которые характеризуются суммой средних величин сезонной компоненты. Чем дальше от 0 значение суммы колебаний сезонной компоненты, тем больше ошибка параметра S. Кстати говоря, автор сообщает о том, что перечень товаров, относящихся к сезонным достаточно велик, но не рассказывает о том, как определить относится ли товар, продаваемый предприятием, к сезонному.
Таким образом, выбирая линию тренда, характеризующую общую тенденцию развития изучаемого явления, необходимо также рассчитывать сезонную компоненту (S) и смотреть на сколько сильно сумма средних значений S отклоняется от 0. Если эта величина близка к 0, то можно утверждать, что продажи действительно имеют сезонный характер и товар, следовательно, можно называть сезонным.
Следующим упущением автора является отсутствие изучения периода сезонных колебаний. С одной стороны — специалисты сами знают: когда начинают расти продажи, а когда падать, но с другой — не у всех товаров сезонные колебания явно выражены. Кроме того, мнение эксперта еще точнее и убедительнее, когда оно подтверждено конкретными данными.
Итак, если мы уже определили, что в модели существует сезонность (сумма значений S близка к 0), то период сезонности рассчитывается как средняя арифметическая между количеством отрицательных и положительных значений сезонной компоненты.
3. Расчет ошибок модели. Изучив поведение сезонной компоненты можно переходить на следующий этап моделирования — расчет ошибок построенной модели. Ошибки рассчитываются по формуле:
E=F-T-S,
при этом вместо значений F подставляются фактические значения объемов продаж.
После нахождения среднеквадратической ошибки модели мы можем делать вывод о точности модели в целом.
4. Построение прогноза. Когда мы определили самую точную модель мы можем перейти на этап прогнозирования, который также описан автором не полностью.
Ведь задача была поставлена в статье «составить прогноз продаж продукции на следующий год по месяцам». А результат, полученный после прогнозирования, характеризуется одним числом. Следовательно, задача, поставленная самим автором, не решена в полном объеме.
Существует также ряд неясностей в ходе дальнейшего прогнозирования:
- Почему взяты данные за январь (Fф t-1 =2 361), тогда как оба исследуемых периода начинаются с июля.
- Как и кем определяется константа сглаживания a. Ведь экспертом, работающим над данной проблемой, является сам автор. А, следовательно, необходим инструментарий определения данной величины.
- Почему не описан инструментарий получения данных доверительного интервала (± 7,8 (руб.)).
- Какие «все возможные сценарии прогноза» автор имеет в виду: те которые зависят от константы сглаживания, или те, которые определяются альтернативными моделями.
Таким образом, автором допущены ошибки использования собственного алгоритма. Эти ошибки позволяют сделать вывод о его несовершенстве или о недостаточной конкретизации самого алгоритма. При этом, следует учесть, что основная идея алгоритма, методики и последовательность действий, выбранные автором, абсолютно верны. Следовательно, доработки требует только алгоритм.
С учетом описанных выше недостатков, можно предположить, что алгоритм должен иметь такой вид:
Таблица 1. Алгоритм прогнозирования объемов продаж
|
№
|
Рассчитываемые показатели
|
Критерий оценки
|
Значение к которому стремиться критерий оценки
|
|
1. Построение модели F=T+S+E
|
|
1.1.
|
Определение трендов, для
построения альтернативных моделей (T1, T2,
T3 …)
|
Количество
|
Чем больше, тем правильнее будет выбор
|
|
1.2.
|
Определение уравнений линий
трендов (вид, который принимает T1,
T2, T3 …, в
зависимости от величин объема продаж)
|
Коэффициент детерминации
|
1,00
|
|
1.3.
|
Определение метода расчета
сезонной компоненты (в нашем случае это расчет средней арифметической)
|
Наличие данных
|
Максимальное количество наблюдаемых периодов
(минимум=2)
|
|
1.4.
|
Определение величин
сезонной компоненты (S)
|
Сумма средних значений
колебаний
|
0,00
|
|
1.5.
|
Определение ошибок модели (E)
|
СКО (среднеквадратическое
отклонение) для каждого периода
|
0,00
|
|
1.6.
|
Определение точности всей
модели
|
[1- СКО для всей
модели]*100%
|
100,00%
|
|
1.7.
|
Определение доверительного
интервала модели
|
(F*[1-СКО];
F*[1+СКО])
|
0,00%
|
|
2. Построение прогноза
|
|
2.1.
|
Определение прогнозных
значений
|
Фактическое значение
будущего периода
|
Фактическое значение
будущего периода (проверка будет осуществлена только по достижении периода)
|
|
2.2.
|
Определение константы
сглаживания
|
|
2.3.
|
Корректировка прогнозных
значений, с использованием экспоненциального
сглаживания
|
Из таблицы видно, что алгоритм не претерпел существенных изменений. Методики, используемые автором в статье, остаются теми же, следовательно, процессуально алгоритм не был усложнен. Однако произведена конкретизация:
- разбивка на этапы моделирования и прогнозирования;
- детализация каждого из этапов;
- определение критериев оценки каждого из этапов;
- определение критических значений критериев оценки. Т.е. чем ближе показатель к величине, указанной в последнем столбце — тем вернее будут модель и прогноз.
С учетом проведенных изменений алгоритма попробует использовать его на примере, предоставленном Кошечкиным С.А.
ПРИМЕР.
Исходные данные: объёмы реализации продукции за два сезона. В качестве исходной информации для прогнозирования была использована информация об объёмах сбыта мороженого "Пломбир" одной из фирм в Нижнем Новгороде. Данная статистика характеризуется тем, что значения объёма продаж имеют выраженный сезонный характер с возрастающим трендом. Исходная информация представлена в табл. 1.
Таблица 2. Фактические объёмы реализации продукции
|
№п.п. |
Месяц |
Объем продаж (руб.) |
№п.п. |
Месяц |
Объем продаж (руб.) |
|
1 |
июль |
8174,40 |
13 |
июль |
8991,84 |
|
2 |
август |
5078,33 |
14 |
август |
5586,16 |
|
3 |
сентябрь |
4507,20 |
15 |
сентябрь |
4957,92 |
|
4 |
октябрь |
2257,19 |
16 |
октябрь |
2482,91 |
|
5 |
ноябрь |
3400,69 |
17 |
ноябрь |
3740,76 |
|
6 |
декабрь |
2968,71 |
18 |
декабрь |
3265,58 |
|
7 |
январь |
2147,14 |
19 |
январь |
2361,85 |
|
8 |
февраль |
1325,56 |
20 |
февраль |
1458,12 |
|
9 |
март |
2290,95 |
21 |
март |
2520,05 |
|
10 |
апрель |
2953,34 |
22 |
апрель |
3248,67 |
|
11 |
май |
4216,28 |
23 |
май |
4637,91 |
|
12 |
июнь |
8227,569 |
24 |
июнь |
9050,3264 |
Задача: составить прогноз продаж продукции на следующий год по месяцам.
Воспользуемся алгоритмом, описанным в таблице 1.
1. Построение модели.
Создадим модели, описывающие продажи мороженого.
Количество создаваемых моделей определяется методом подбора. При этом следует учитывать, что большее количество построенных моделей даст возможность выбрать наиболее точную модель, описывающую продажи продукции.
1.1. Изначально, нам не известно какое из уравнений трендов даст наилучший результат, поэтому на данном этапе моделирования целесообразнее всего использовать все линии тренда, которые может строить программный продукт MS Excel:
- линейный тренд;
- логарифмический тренд;
- полиномиальный тренд (возьмем 6-ю степень, чтобы увидеть ошибки, допущенные ранее);
- степенной тренд;
- экспоненциальный тренд.
Для простоты и большей наглядности данного примера, а также отражения сути предложенного алгоритма ограничимся выбором трех линий тренда. Заранее отметим, что линии тренда выбраны случайным образом. Полиномиальный и линейный тренд выбраны, т.к. Кошечкин С.А. отдал предпочтение полиному, выбирая между линейным и полиномиальным трендом. И еще один тренд взят на личное усмотрение —логарифмический тренд.
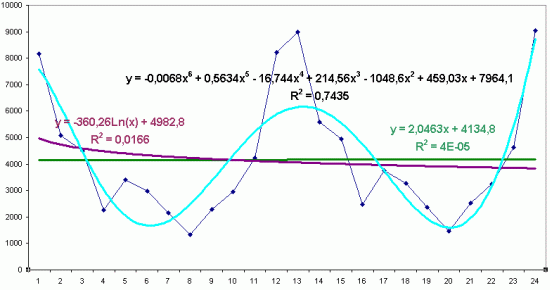
Рис. 1. Выбранные линии тренда
По коэффициентам детерминации видно, что наиболее предпочтителен полином, а наименее — линейный тренд. Но т.к. коэффициент детерминации (R2) не определяет точность всей модели, то выбор тренда на этом этапе мы сделать не можем.
1.2. Уравнения линий тренда принимают вид, указанный на рисунке 1. Чтобы получить цифровые значения линий тренда за каждый месяц, необходимо внести уравнения, показанные на графике в ячейки MS Excel в виде формул, где Х (независимая компонента) — это последовательность чисел от 1 до 24 (см. рисунок 2). А Y — это значения уравнения линии тренда для каждого из Х.
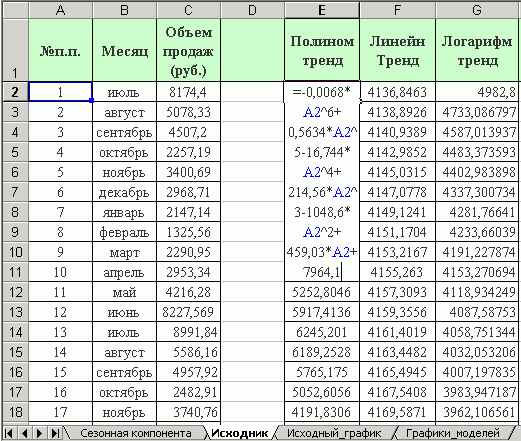
Рис. 2. Уравнение полиномиальной линии тренда в формате MS Excel
Аналогично полиному, рассчитаем линейный и логарифмический тренды. Результаты расчетов в таблице 3.
Таблица 3. Данные полученные с помощью уравнений линий трендов
|
№п.п.
|
Месяц
|
Полином тренд
|
Линейный Тренд
|
Логарифм тренд
|
|
1
|
июль
|
7572,9026
|
4136,8463
|
4982,8
|
|
2
|
август
|
6153,9296
|
4138,8926
|
4733,086797
|
|
3
|
сентябрь
|
4472,595
|
4140,9389
|
4587,013937
|
|
4
|
октябрь
|
3017,0648
|
4142,9852
|
4483,373593
|
|
5
|
ноябрь
|
2053,625
|
4145,0315
|
4402,983898
|
|
6
|
декабрь
|
1677,1536
|
4147,0778
|
4337,300734
|
|
7
|
январь
|
1856,6966
|
4149,1241
|
4281,76641
|
|
8
|
февраль
|
2476,148
|
4151,1704
|
4233,66039
|
|
9
|
март
|
3370,0338
|
4153,2167
|
4191,227874
|
|
10
|
апрель
|
4354,4
|
4155,263
|
4153,270694
|
|
11
|
май
|
5252,8046
|
4157,3093
|
4118,934249
|
|
12
|
июнь
|
5917,4136
|
4159,3556
|
4087,58753
|
|
13
|
июль
|
6245,201
|
4161,4019
|
4058,751344
|
|
14
|
август
|
6189,2528
|
4163,4482
|
4032,053206
|
|
15
|
сентябрь
|
5765,175
|
4165,4945
|
4007,197835
|
|
16
|
октябрь
|
5052,6056
|
4167,5408
|
3983,947187
|
|
17
|
ноябрь
|
4191,8306
|
4169,5871
|
3962,106561
|
|
18
|
декабрь
|
3375,504
|
4171,6334
|
3941,514671
|
|
19
|
январь
|
2835,4718
|
4173,6797
|
3922,036413
|
|
20
|
февраль
|
2824,7
|
4175,726
|
3903,557491
|
|
21
|
март
|
3594,3066
|
4177,7723
|
3885,980347
|
|
22
|
апрель
|
5365,6976
|
4179,8186
|
3869,221046
|
|
23
|
май
|
8297,807
|
4181,8649
|
3853,206854
|
|
24
|
июнь
|
12449,4408
|
4183,9112
|
3837,874327
|
Кстати говоря, значения полиномиального тренда, полученные при работе, совершенно не совпадают с данными, которые получил Кошечкин С.А. в своей статье. Если кто-нибудь сможет подсказать как он рассчитывал данные полиномиального тренда, буду очень признателен.
1.3. В случае, если осуществляется не тактический, а стратегический анализ, т.е. собраны данные хотя бы за 4 сезона, то сезонная компонента (S) может быть представлена отдельными уравнениями, что увеличит точность S. Не следует забывать, что это усложнит процесс моделирования. Но т.к. исходные данные имеются только за 2 периода, то выбор средних величин в расчете сезонных компонент является оптимальным.
1.4. Используя методику Кошечкина С.А., рассчитываем сезонную компоненту для каждого из уравнений тренда. Из фактических данных вычитаем значения линий тренда для каждого из сезонов. Имеем 3 таблицы (табл. 4-6).
Таблица 4. Расчет сезонной компоненты для модели с полиномиальным трендом
|
Месяц
|
Сезон 1
|
Сезон 2
|
Среднее
|
Сезонная компонента
|
|
июль
|
601,4974
|
2746,639
|
1674,068
|
2278,748
|
|
август
|
-1075,5996
|
-603,093
|
-839,346
|
-234,667
|
|
сентябрь
|
34,605
|
-807,255
|
-386,325
|
218,3544
|
|
октябрь
|
-759,8748
|
-2569,7
|
-1664,79
|
-1060,11
|
|
ноябрь
|
1347,065
|
-451,071
|
447,9972
|
1052,677
|
|
декабрь
|
1291,5564
|
-109,924
|
590,8162
|
1195,496
|
|
январь
|
290,4434
|
-473,622
|
-91,5892
|
513,0902
|
|
февраль
|
-1150,588
|
-1366,58
|
-1258,58
|
-653,905
|
|
март
|
-1079,0838
|
-1074,26
|
-1076,67
|
-471,991
|
|
апрель
|
-1401,06
|
-2117,03
|
-1759,04
|
-1154,36
|
|
май
|
-1036,5246
|
-3659,9
|
-2348,21
|
-1743,53
|
|
июнь
|
2310,1554
|
-3399,11
|
-544,48
|
60,19986
|
|
ИТОГО:
|
-7256,15
|
0
|
В таблице 4 четко видно, что отклонение сезонных колебаний модели с полиномиальным трендом от 0 весьма велико и утверждать, что в модели выявлена сезонность, мы не можем. А если предполагать, что сезонность существует, исходя из экономических соображений и знаний специфики рынка и товара, то ошибка модели в итоге вырастет. Таким образом, высокая точность модели, полученная благодаря выбору полинома, будет нейтрализована низкой точностью сезонной компоненты. Чтобы проверить данное утверждение, построим полностью модель с полиномиальным трендом.
Таблица 5. Расчет сезонной компоненты для модели с линейным трендом
|
Месяц
|
Сезон 1
|
Сезон 2
|
Среднее
|
Сезонная компонента
|
|
июль
|
4037,5537
|
4830,438
|
4433,996
|
4433,981
|
|
август
|
939,4374
|
1422,712
|
1181,075
|
1181,059
|
|
сентябрь
|
366,2611
|
792,4255
|
579,3433
|
579,3281
|
|
октябрь
|
-1885,7952
|
-1684,63
|
-1785,21
|
-1785,23
|
|
ноябрь
|
-744,3415
|
-428,827
|
-586,584
|
-586,6
|
|
декабрь
|
-1178,3678
|
-906,053
|
-1042,21
|
-1042,23
|
|
январь
|
-2001,9841
|
-1811,83
|
-1906,91
|
-1906,92
|
|
февраль
|
-2825,6104
|
-2717,61
|
-2771,61
|
-2771,62
|
|
март
|
-1862,2667
|
-1657,72
|
-1759,99
|
-1760,01
|
|
апрель
|
-1201,923
|
-931,149
|
-1066,54
|
-1066,55
|
|
май
|
58,9707
|
456,0451
|
257,5079
|
257,4927
|
|
июнь
|
4068,2134
|
4866,415
|
4467,314
|
4467,299
|
|
ИТОГО:
|
0,1827
|
0
|
В таблице 5 по сумме средних величин видно, что наблюдается сезонность колебаний, т.к. сумма средних величин сезонных колебаний близка к 0.
Чтобы довести средние колебания до 0, необходимо итоговую сумму средних разделить на количество периодов в сезоне (в нашем случае — это 12). Полученный результат вычитаем из значений среднего по каждому периоду. В итоге — сумма колебаний составит абсолютный 0.
Таблица 6. Расчет сезонной компоненты для модели с логарифмическим трендом
|
Месяц
|
Сезон 1
|
Сезон 2
|
Среднее
|
Сезонная компонента
|
|
июль
|
3191,6
|
4933,089
|
4062,344
|
4062,386
|
|
август
|
345,2432033
|
1554,107
|
949,675
|
949,7166
|
|
сентябрь
|
-79,81393688
|
950,7222
|
435,4541
|
435,4957
|
|
октябрь
|
-2226,183593
|
-1501,04
|
-1863,61
|
-1863,57
|
|
ноябрь
|
-1002,293898
|
-221,347
|
-611,82
|
-611,779
|
|
декабрь
|
-1368,590734
|
-675,935
|
-1022,26
|
-1022,22
|
|
январь
|
-2134,62641
|
-1560,19
|
-1847,41
|
-1847,36
|
|
февраль
|
-2908,10039
|
-2445,44
|
-2676,77
|
-2676,73
|
|
март
|
-1900,277874
|
-1365,93
|
-1633,1
|
-1633,06
|
|
апрель
|
-1199,930694
|
-620,551
|
-910,241
|
-910,199
|
|
май
|
97,34575098
|
784,7031
|
441,0244
|
441,066
|
|
июнь
|
4139,98147
|
5212,452
|
4676,217
|
4676,258
|
|
ИТОГО:
|
-0,49899
|
0
|
По данным таблицы 6 можно утверждать, что в модели с логарифмическим трендом также существуют сезонные колебания, т.к. сумма средних близка к 0.
Рассчитанные сезонные компоненты для каждого из уравнений тренда при прогнозировании просто переносятся на соответствующие месяцы прогнозного периода.
1.5. Получив 3 сезонных компоненты (S) с 3 уравнениями тренда (T), мы можем рассчитать ошибки построенных моделей (E). Для этого из исходных значений задачи необходимо отнять сумму S+T, E=F-(S+T). Данные расчета представлены в таблице 7.
Таблица 7. Значения моделей (T+S) и их ошибок (E)
|
№
|
Месяц
|
ФАКТ
|
значение полнином. модели
|
значение лин. модели
|
значение логарифм. модели
|
Ошибки полином. модели
|
Ошибки лин. модели
|
Ошибки логарифм. модели
|
|
1
|
июль
|
8174,4
|
9851,65
|
8570,83
|
9045,19
|
-1677,25
|
-396,43
|
-870,79
|
|
2
|
август
|
5078,33
|
5919,26
|
5319,95
|
5682,80
|
-840,93
|
-241,62
|
-604,47
|
|
3
|
сентябрь
|
4507,2
|
4690,95
|
4720,27
|
5022,51
|
-183,75
|
-213,07
|
-515,31
|
|
4
|
октябрь
|
2257,19
|
1956,96
|
2357,76
|
2619,80
|
300,23
|
-100,57
|
-362,61
|
|
5
|
ноябрь
|
3400,69
|
3106,30
|
3558,43
|
3791,21
|
294,39
|
-157,74
|
-390,52
|
|
6
|
декабрь
|
2968,71
|
2872,65
|
3104,85
|
3315,08
|
96,06
|
-136,14
|
-346,37
|
|
7
|
январь
|
2147,14
|
2369,79
|
2242,20
|
2434,40
|
-222,65
|
-95,06
|
-287,26
|
|
8
|
февраль
|
1325,56
|
1822,24
|
1379,55
|
1556,93
|
-496,68
|
-53,99
|
-231,37
|
|
9
|
март
|
2290,95
|
2898,04
|
2393,21
|
2558,17
|
-607,09
|
-102,26
|
-267,22
|
|
10
|
апрель
|
2953,34
|
3200,04
|
3088,71
|
3243,07
|
-246,70
|
-135,37
|
-289,73
|
|
11
|
май
|
4216,28
|
3509,27
|
4414,80
|
4560,00
|
707,01
|
-198,52
|
-343,72
|
|
12
|
июнь
|
8227,569
|
5977,61
|
8626,65
|
8763,85
|
2249,96
|
-399,09
|
-536,28
|
|
13
|
июль
|
8991,84
|
8523,95
|
8595,38
|
8121,14
|
467,89
|
396,46
|
870,70
|
|
14
|
август
|
5586,16
|
5954,59
|
5344,51
|
4981,77
|
-368,43
|
241,65
|
604,39
|
|
15
|
сентябрь
|
4957,92
|
5983,53
|
4744,82
|
4442,69
|
-1025,61
|
213,10
|
515,23
|
|
16
|
октябрь
|
2482,91
|
3992,50
|
2382,31
|
2120,38
|
-1509,59
|
100,60
|
362,53
|
|
17
|
ноябрь
|
3740,76
|
5244,51
|
3582,99
|
3350,33
|
-1503,75
|
157,77
|
390,43
|
|
18
|
декабрь
|
3265,58
|
4571,00
|
3129,41
|
2919,29
|
-1305,42
|
136,17
|
346,29
|
|
19
|
январь
|
2361,85
|
3348,56
|
2266,76
|
2074,67
|
-986,71
|
95,09
|
287,18
|
|
20
|
февраль
|
1458,12
|
2170,80
|
1404,10
|
1226,83
|
-712,68
|
54,02
|
231,29
|
|
21
|
март
|
2520,05
|
3122,32
|
2417,76
|
2252,92
|
-602,27
|
102,29
|
267,13
|
|
22
|
апрель
|
3248,67
|
4211,33
|
3113,27
|
2959,02
|
-962,66
|
135,40
|
289,65
|
|
23
|
май
|
4637,91
|
6554,28
|
4439,36
|
4294,27
|
-1916,37
|
198,55
|
343,64
|
|
24
|
июнь
|
9050,33
|
12509,64
|
8651,21
|
8514,13
|
-3459,31
|
399,12
|
536,19
|
На основании рассчитанных ошибок (E) рассчитаем среднеквадратическое отклонение (СКО) для каждого из периодов (см. Таблицу 8). Формула расчета приведена в работе Кошечкина С.А.
Таблица 8. Среднеквадратическое отклонение значений модели от фактических данных
|
№
|
Месяц
|
СКО полином. модели
|
СКО лин. модели
|
СКО логарифм. модели
|
|
1
|
июль
|
0,0290
|
0,0021
|
0,0093
|
|
2
|
август
|
0,0202
|
0,0021
|
0,0113
|
|
3
|
сентябрь
|
0,0015
|
0,0020
|
0,0105
|
|
4
|
октябрь
|
0,0235
|
0,0018
|
0,0192
|
|
5
|
ноябрь
|
0,0090
|
0,0020
|
0,0106
|
|
6
|
декабрь
|
0,0011
|
0,0019
|
0,0109
|
|
7
|
январь
|
0,0088
|
0,0018
|
0,0139
|
|
8
|
февраль
|
0,0743
|
0,0015
|
0,0221
|
|
9
|
март
|
0,0439
|
0,0018
|
0,0109
|
|
10
|
апрель
|
0,0059
|
0,0019
|
0,0080
|
|
11
|
май
|
0,0406
|
0,0020
|
0,0057
|
|
12
|
июнь
|
0,1417
|
0,0021
|
0,0037
|
|
13
|
июль
|
0,0030
|
0,0021
|
0,0115
|
|
14
|
август
|
0,0038
|
0,0020
|
0,0147
|
|
15
|
сентябрь
|
0,0294
|
0,0020
|
0,0134
|
|
16
|
октябрь
|
0,1430
|
0,0018
|
0,0292
|
|
17
|
ноябрь
|
0,0822
|
0,0019
|
0,0136
|
|
18
|
декабрь
|
0,0816
|
0,0019
|
0,0141
|
|
19
|
январь
|
0,0868
|
0,0018
|
0,0192
|
|
20
|
февраль
|
0,1078
|
0,0015
|
0,0355
|
|
21
|
март
|
0,0372
|
0,0018
|
0,0141
|
|
22
|
апрель
|
0,0523
|
0,0019
|
0,0096
|
|
23
|
май
|
0,0855
|
0,0020
|
0,0064
|
|
24
|
июнь
|
0,0765
|
0,0021
|
0,0040
|
|
Среднее значение:
|
0,0495
|
0,0019
|
0,0134
|
1.6. Рассчитав среднее значение СКО, полученных для каждой модели, рассчитаем точность по формуле:
(точность модели) = [1 - (среднее значение СКО)]*100%
Точность модели с полиномиальным трендом = 95.05%
Точность модели с линейным трендом = 99.81%
Точность модели с логарифмическим трендом = 98.66%
Таким образом, высокой точностью обладают все 3 модели (см. рисунок 3).
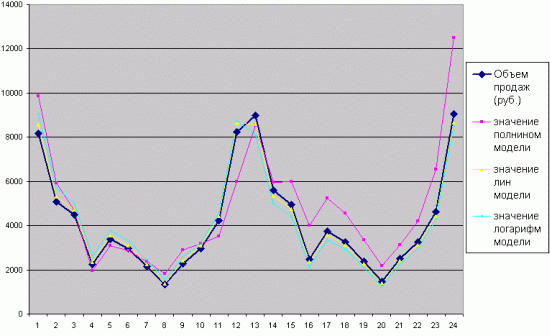
Рис. 3. Модели, построенные на основании различных линий тренда
Т.к. в случае, если точность модели колеблется в районе 90%-100%, то можно утверждать, что модель достаточно точная. Однако, модель с линейным трендом является наиболее точной, т.к. ее показатель точности наиболее высокий. Следовательно, прогноз, сделанный на основании данных линейной модели будет наиболее точным. И только на данном этапе моделирования мы можем сделать окончательный вывод о предпочтительности модели. Выбрав модель с линейным трендом, в дальнейшем, будем работать только с ней.
1.7. Чтобы построить доверительный интервал воспользуемся данными СКО для модели с линейным трендом (СКО=0,0019). Доверительный интервал примет вид:
(F*[1-СКО];F*[1+СКО])
Данные такого расчета приведены в таблице 9.
Таблица 9. Доверительный интервал для модели с линейным трендом
|
F-СКО
|
F+СКО
|
|
8552,491
|
8589,163
|
|
5308,978
|
5330,926
|
|
4710,649
|
4729,885
|
|
2353,467
|
2362,047
|
|
3551,439
|
3565,425
|
|
3098,882
|
3110,822
|
|
2238,172
|
2246,232
|
|
1377,434
|
1381,66
|
|
2388,838
|
2397,576
|
|
3082,779
|
3094,645
|
|
4405,875
|
4423,729
|
|
8608,192
|
8645,117
|
|
8577,096
|
8613,669
|
|
5333,581
|
5355,434
|
|
4735,252
|
4754,393
|
|
2378,065
|
2386,56
|
|
3576,04
|
3589,935
|
|
3123,482
|
3135,333
|
|
2262,768
|
2270,747
|
|
1402,024
|
1406,181
|
|
2413,435
|
2422,09
|
|
3107,379
|
3119,157
|
|
4430,477
|
4448,238
|
|
8632,797
|
8669,623
|
2. Построение прогноза.
Определив наиболее точную модель, можем построить прогноз изменений продаж мороженого на 3-й сезон.
2.1. Для расчета прогнозных значений в пакете MS Excel, укажем условия прогнозирования:
- трендовая компонента (Т) зависит от последовательности чисел от 1 до 24. Следовательно, чтобы построить прогноз, необходимо продолжить эту последовательность до 36. Значения трендовой компоненты MS Excel рассчитает в автоматическом режиме. Достаточно выделить последнюю ячейку 24-го месяца и зажав черный квадратик в нижнем правом углу ячейки протащить выделение до 36 периода. В итоге получим трендовую компоненту Т. (Сделайте аналогичную операцию с полиномом и увидите: почему книжки не рекомендуют использовать полиномы в прогнозировании — уже в апреле 3-го сезона наши продавцы мороженого станут !!! банкротом !!!)
- сезонная компонента (S) рассчитанная для модели, остается неизменной для 25-36 месяцев. Выделим в MS Excel сезонную компоненту и скопируем на периоды 25-36.
- Для учета ошибок воспользуемся доверительным интервалом модели, рассчитанным для прогнозных значений. Доверительный интервал отражает в каких пределах может колебаться ошибка прогнозных значений.
Таблица 10. Расчет прогнозных значений модели с линейным трендом
|
№
|
Месяцы
|
Линейный Тренд (Т)
|
Сезонная компонента (S)
|
Прогнозные значения линейной модели (F)
|
Доверительный интервал
|
|
-
|
+
|
|
25
|
июль
|
4185,9575
|
4433,981
|
8619,94
|
8193,058
|
9046,82
|
|
26
|
август
|
4188,0038
|
1181,059
|
5369,06
|
5103,174
|
5634,95
|
|
27
|
сентябрь
|
4190,0501
|
579,3281
|
4769,38
|
4533,187
|
5005,57
|
|
28
|
октябрь
|
4192,0964
|
-1785,23
|
2406,87
|
2287,674
|
2526,06
|
|
29
|
ноябрь
|
4194,1427
|
-586,6
|
3607,54
|
3428,889
|
3786,20
|
|
30
|
декабрь
|
4196,189
|
-1042,23
|
3153,96
|
2997,771
|
3310,15
|
|
31
|
январь
|
4198,2353
|
-1906,92
|
2291,31
|
2177,842
|
2404,78
|
|
32
|
февраль
|
4200,2816
|
-2771,62
|
1428,66
|
1357,908
|
1499,41
|
|
33
|
март
|
4202,3279
|
-1760,01
|
2442,32
|
2321,369
|
2563,27
|
|
34
|
апрель
|
4204,3742
|
-1066,55
|
3137,82
|
2982,431
|
3293,22
|
|
35
|
май
|
4206,4205
|
257,4927
|
4463,91
|
4242,85
|
4684,98
|
|
36
|
июнь
|
4208,4668
|
4467,299
|
8675,77
|
8246,121
|
9105,41
|
Если представить графически прогноз, рассчитанный с помощью выбранной модели, то результаты прогнозирования примут вид:
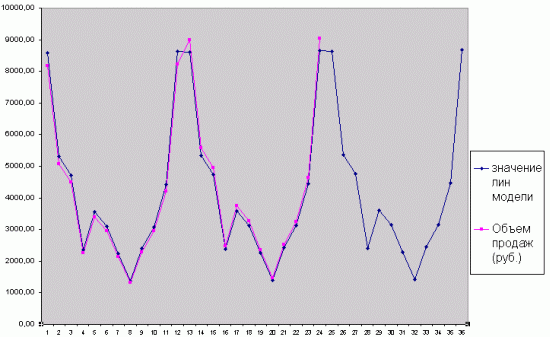
Рис. 4. Прогноз продаж мороженого в третьем сезоне
2.2. Определять константу сглаживания можно несколькими способами:
- самостоятельный расчет индексов стабильности экономики и учет всех рисков изменения конъюнктуры рынка и отрасли, в которой находится предприятие. При этом возможно использование и внутренней информации предприятия, и информации государственных статистических органов.
- использование ранее рассчитанных показателей стабильности рынка. Таких как, динамика индекса цен, индекс инфляции, показатели покупательской способности, банковская учетная ставка и т.д.
Возникла проблема в доведении примера до логического конца — отсутствие статистической информации о Российской Федерации и, тем более, о Нижнем Новгороде.
Так что, могу повествовать лишь на идейном уровне. Т.к. Кошечкин С.А. утверждает, что константа сглаживания — это «вероятность сохранения существующей рыночной конъюнктуры», то
а = 1 - (учетная ставка центрального банка)
Следует отметить, что такой способ определения константы сглаживания для сезонного товара не совсем корректен, т.к. в каждом месяце конъюнктура разная из-за сезонности товара. Т.е. необходим поправочный коэффициент, который рассчитывается на основании статистических данных об отрасли.
2.3. Т.к. константу сглаживания рассчитать не получилось, то и скорректировать прогноз тоже не представляется возможным.
Таким образом, мы пришли к выводу, что:
- при моделировании хозяйственного процесса ВСЕГДА необходимо строить несколько моделей, чтобы сравнить результаты;
- тактический и стратегический анализ сильно отличаются. И если при построении прогноза на 1 год можно воспользоваться средними величинами при определении сезонных колебаний, то при создании стратегического плана необходимы более точные модели, а значит — более сложные методы;
- полином использовать в моделировании хозяйственных процессов крайне рискованно, т.к. несмотря на высокую точность трендовой компоненты можно получить данные искаженные данные;
- определить точность модели можно только после расчета и тренда, и сезонной компоненты;
- константа сглаживания формируется на основании конкретных данных, а не на основании «экспертных оценок»;
- в рассмотренном примере выбор линейного тренда более предпочтителен, чем выбор полинома;
- необходим дополнительный анализ внешней среды для построения более адекватной модели (с использованием экспоненциального сглаживания).
Авторская справка:
Бондаренко А.В.
Специалист-аналитик по исследованию товарного рынка ООО "УБС"
Магистрант кафедры "Прикладная экономика" Донецкого Национального Университета (Украина)
|
 |